BASICS OF THE BEAUTIFUL FORMULA LANGUAGE

THE BEAUTIFUL FORMULA LANGUAGE allows to create new compositions and to notate already existing paintings.

We are constantly working on the improvement of THE BEAUTIFUL FORMULA LANGUAGE. Please, feel free to send us your suggestion, comment or any kind of question.

Oleksiy Koval and THE BEAUTIFUL FORMULA COLLECTIVE

download as PDF

SIGNS AND SYMBOLS

U unit
M meter
A area
T takt
R rhythmical motive
E element
P procedure
# entry

* hits the meter
[ ] within the same area
#(n) number of entries
∞ number of entries flexible
(n) size of unit
≈ is corresponding for all elements
\ bigger than
/ less than
|| order fixed
> n occupy n
-> go to
{ n out of n possible
+ has to touch
_ has not to touch
≠ not
V vertical
H horizontal
F flexibel
ⁿ ordinal number
L line
{ n } polygon with n edges
æ all
| or

U
unit

The unit defines the basic size of any kind of mark on the surface.
1 is the smallest size of a mark, 2 is twice as big, 3 is three times bigger and so forth…

Examples: 1,2,3

M
meter

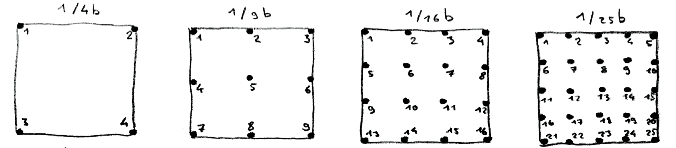
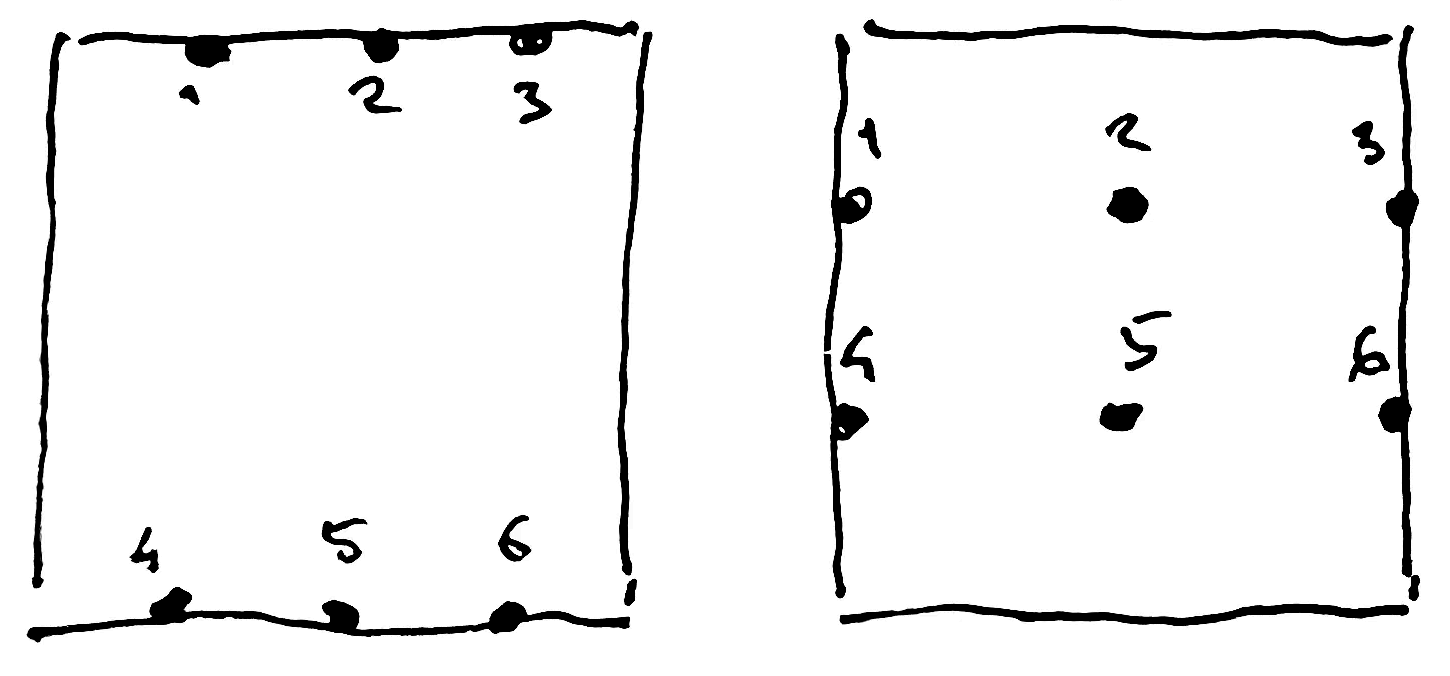
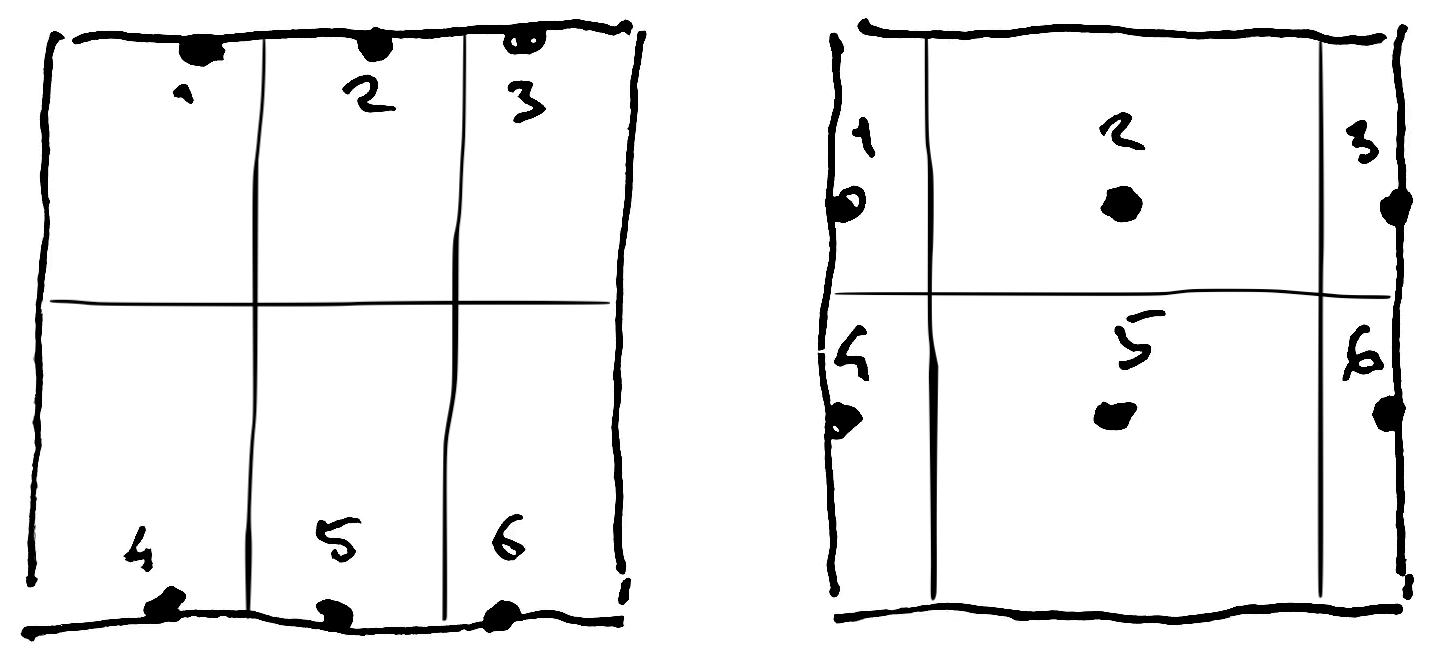
The meter is a fixed point with a surrounding area.
The meter is used to accomplish an equal partition of the surface.
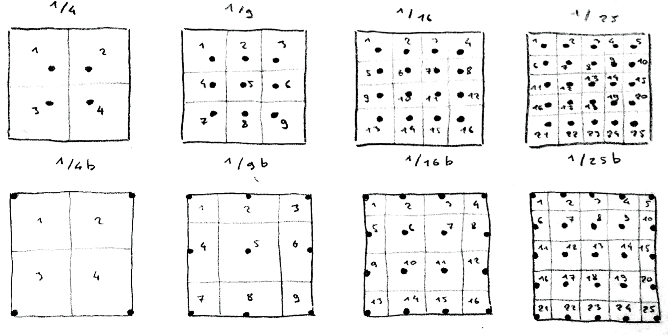
A meter is numbered from left to right and top to bottom.

Examples: 1/4, 1/9, 1/16, 1/25

Meters with the additional letter b include the surface border and the four corners.

Examples: 1/4b, 1/9b, 1/16b, 1/25b

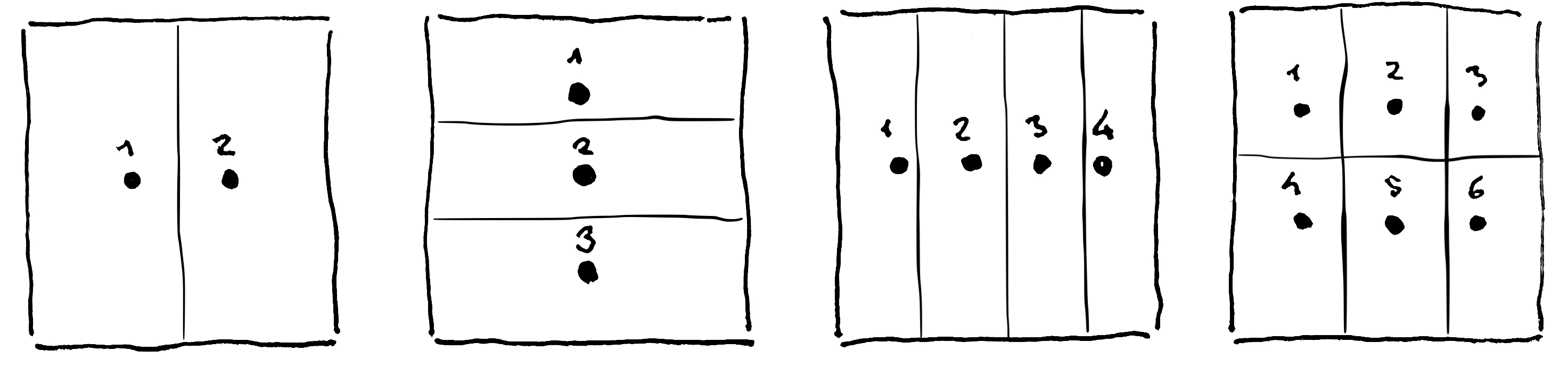
The asymmetrical meters divide a surface by a different number of meter intervals horizontally H and vertically V.

Examples:

M 1/2 H2 V1
M 1/3 H1 V3
M 1/4 H4 V1
M 1/6 H3 V2

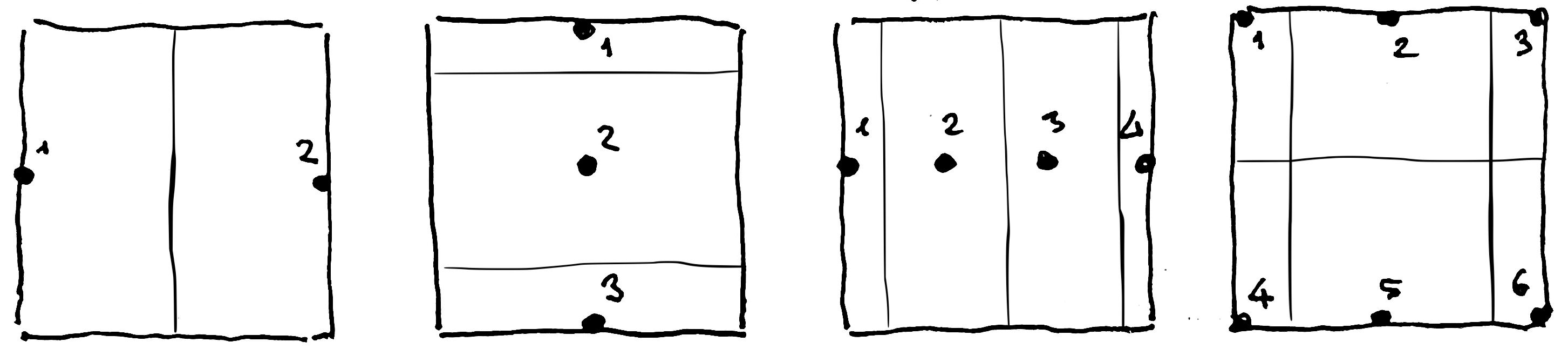
The asymmetrical meters with the additional letter b include the surface border and the four corners.

Examples:

M 1/2b H2 V1
M 1/3b H1 V3
M 1/4b H4 V1
M 1/6b H3 V2

The asymmetrical meters with the additional letters Hb include only the horizontal surface border and Vb include only the vertical surface border.

Examples:

M 1/6Hb H3 V2
M 1/6Vb H3 V2

A
area

The area surrounds the meter and is defined by the rows and columns between meters.
The area and its meter have the same numbering.

Examples: 1/4, 1/9, 1/16, 1/25 & 1/4b, 1/9b, 1/16b, 1/25b

Examples:

M 1/2 H2 V1, A 1/2
M 1/3 H1 V3, A 1/3
M 1/4 H4 V1, A 1/4
M 1/6 H3 V2, A 1/6

Examples:

M 1/2b H2 V1, A 1/2b
M 1/3b H1 V3, A 1/3b
M 1/4b H4 V1, A 1/4b
M 1/6b H3 V2, A 1/6b

Examples:

M 1/6Hb H3 V2, A 1/6b
M 1/6Vb H3 V2, A 1/6b

T
takt

The takt is a fixed number of units during one single entry.

Examples: A T2, B T3, C T4, D T5

R
rhythmical motive

The rhythmical motive is a fixed sequence of units during one single entry.

Examples: 2,2,3,1 & 1,2,1,3,1,5 

E
element

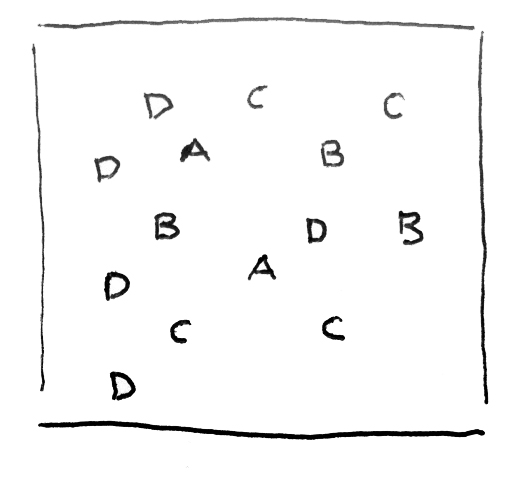
The element is a unique character of a unit.
Elements are named with a, b, c …

Examples:

M 1/4
R 2,2,3,1
E a,b,c,d

P
procedure

The procedure defines the painting process.

Examples:

M 1/4
R 1,2,1,3,1,5
E a,b,c,d,e,f
P *a1,b2,c1,d3,e1,f5

#
entry

The entry defines how often each element can participate.

Examples:

M 1/4
R 1,2,1,3,1,5
E a,b,c,d,e,f
P *a1,b2,c1,d3,e1,f5 #3

*
hits the meter

M 1/4
R 2,2,3,1
E a,b,c,d
P *a2,*b2,*c3,*d1

[ ]
within the same area

M 1/4
R 2,2,3,1
E a,b,c,d
P
[*a2,b2,c3,d1]
[*b2,c2,d3,a1]
[*c2,d2,a3,b1]
[*d2,a2,b3,c1]

#(n)
number of entries

M 1/9
R 2,2,3,1
E a,b,c,d
P
[*a] #(1)
[*b] #(2)
[*c] #(2)
[*d] #(4)

∞
number of entries flexible

M 1/4
R 2,2,3,1
E a,b
P
a #∞
b M4 [*2,2,3,1] #1

(n)
size of unit

M 1/4
R –,–,–,–,– (1-5) (size of unit can vary from 1-5)
E a
P [*a] > 1{M1/4

≈
is corresponding for all elements

M 1/4
A 1/4
R 2,2,3,1
E a,b,c,d ≈
P
a A1[*2,2,3,1]
b A2[*2,2,3,1]
c A3[*2,2,3,1]
d A4[*2,2,3,1]

\
bigger than

A 1/4
E a
P [*-\(3),2,2,3,1] > 1{A1/4

/
less than

A 1/4
E a
P [*-/(1),2,2,3,1] > 1{A1/4

||
order fixed

M 1/4
R 1,1,1,2,3
E |a,b,c,d| (the entry of the elements has to be in the same order)
P
M1 [*a]
M4 [*a,b,c,d]

>
n occupy n

M 1/4, 1/9
R 2,2,3,1
E a,b
P
M 1/4 [*a] > M4
M 1/9 [*b] > M5

{
n out of n possible

M 1/4
R 2,2,3,1
E a,b
P
[*a]
[*a]
[*a]
[*a,b] b > 1{4[a]
b has to choose one of the 4 areas already taken by a

+
has to touch

M 1/4
R 1,2,1,3,1,5
E |a,b,c|
P *a+b+c

_
has not to touch

A 1/9b
R 2,2,3,1
E a,b,c,d ≈
P
a_b_c_d
a A9[2+2+3+1]
b A9[2+2+3+1]
c A9[2+2+3+1]
d A9[2+2+3+1]

≠
not

M 1/4
R 2,2,3,1
E |a,b|
P
A1 [≠*a]
A2 [≠*a]
A3 [≠*a]
A4 [≠*a]
b M1 *2, M2 *2, M3 *3, M4 *1

V
vertical

M 1/9
R 2,2,3,1
E a
P a > 3{1/9 [*a]+[*a]+[*a] V

H
horizontal

M 1/9
R 2,2,3,1
E a
P a > 3{1/9 [*a]+[*a]+[*a] H

F
flexibel

M 1/9
R 2,2,3,1
E a
P a > 3{1/9 [*a]+[*a]+[*a] F

ⁿ
ordinal number

A
A¹ 1/4
A² 1/9
R 2,2,3,1 & 1,2,1,3,1,5
E a
P
a A¹ A3 [*2,2,3,1]
a A² A8 [*1,2,1,3,1,5]

M 1/4
R 1,2,1,3,1,5
E a¹ a²
P
a¹ M1 [*1,2,1,3,1,5]
a² (2\a¹) M4 [*1,2,1,3,1,5]

L
line

A 1/144 (L 1-12)
E a
P
L1 A2 [(1)]
L2 A1 [(3)]
L3 A6 [(2)]
L12 A11 [(2)]

{ n }
polygon with n edges

A 1/4, 1/9, 1/16
E a,b,c
P
a{3} A1/4
b{4} A1/9
c{5} A1/16

æ
all

M 1/4 & 1/9
E a
P a(-)+*æ13M

|
or

M 1/4 & 1/9
E a,b
P
a|b(-)+m1(1/4)
a|b(-)+m3(1/9)